ОљОЋОЏОюОЋОАОЎОЎОћ ОЋОЊОњОЎОъОћ
ОъОЋОЕОњОЎ ОЎОАОЋОЊ :
- ОљОЋОЏОюОЋОАОЎОЎОћ: ОЏОюОю ОћОцОеОўОЎОЮ ОћОеОюОЋОЋОаОўОЎОЎОЮ ОюОъОЊОЎОЊОћ ОЋОЉОЊОЎОДОћ ОЕОю ОАОЋОњОЎОћ ОДОЋОаОДОеОўОЎОф ОљОЋ ОаОЋОњОбОЎОЮ ОюОъОЌОДОе. (ОюОљ ОеОД ОљОаОЕОЎОЮ! ОљОЮ ОЉОЋОЊОДОЎОЮ ОъОЕОћОЋ ОбОю ОЏОфОЉОЋОф ОЉОбОЎОфОЋОЪ, ОћОЏОфОЉОЋОф ОћОЪ ОћОљОЋОЏОюОЋОАОЎОћ).
- ОъОАОњОеОф ОћОЊОњОЎОъОћ: ОъОДОЋОе ОъОъОаОЋ ОаОЎОфОЪ ОюОЉОдОб ОљОф ОћОЊОњОЎОъОћ – ОюОљ ОцОбОЮ ОЎОЕОаОЋ ОцОбОе ОЉОЎОЪ ОъОАОњОеОф ОћОЊОњОЎОъОћ ОюОЉОЎОЪ ОћОљОЋОЏОюОЋОАОЎОЎОћ.
- ОъОЊОњОЮ: ОДОЉОЋОдОф ОцОеОўОЎОЮ ОћОъОћОЋОЋОЎОЮ ОЌОюОД ОъОљОЋОЏОюОЋОАОЎОЎОћ ОеОЌОЉОћ ОЎОЋОфОе, ОбОюОЎОћ ОъОфОЉОдОб ОћОъОЌОДОе. ОъОЊОњОЮ ОљОЎОаОЋ ОЌОЎОЎОЉ ОюОћОЎОЋОф ОъОЎОЎОдОњ, ОљОџ ОЏОЏОќОћ ОЎОЕ ОюОЋ ОцОЌОЋОф ОбОеОџ ОЉОћОАОДОћ ОбОю ОћОљОЋОЏОюОЋОАОЎОЎОћ ОЏОЋОюОћ. ОъОЊОњОЮ ОъОЎОЎОдОњ ОЕОЎОЏОЋОю ОюОЕОъОЕ ОЏОъОЋОЊОю ОЕОю ОћОљОЋОЏОюОЋОАОЎОЎОћ ОъОљОцОЕОе ОћОАОДОћ ОаОЏОЋОаОћ ОЎОЋОфОе ОбОю ОљОЋОЏОюОЋОАОЎОЎОћ ОеОЌОЉОћ.
- ОЊОњОЎОъОћ: ОЊОњОЎОъОћ ОћОЎОљ ОцОеОЋОдОЊОЋОеОћ ОЕОЉОбОќОеОфОћ ОЉОЋОЌОеОЎОЮ ОљОф ОћОљОаОЕОЎОЮ ОЕОЎОЕОфОфОцОЋ ОЉОъОЊОњОЮ.
ОъОЊОњОЮ ОъОЎОЎОдОњ ОћОЋОљ ОъОДОЉОЦ ОЕОюОџ ОаОЉОЊОДОЎОЮ, ОфОдОцОЎОЋОф ОљОЋ ОъОДОеОЎ ОЉОЋОЌОЪ ОЕОфОЏОЋОаОЋОфОЎОЋ ОъОЕОДОцОЋОф ОљОф ОфОЏОЋОаОЋОф ОћОљОЋОЏОюОЋОАОЎОЎОћ ОъОъОаОЋ ОаОюОДОЌ.
- ОъОЊОњОЮ ОћОАОфОЉОеОЋОфОЎ: ОъОЊОњОЮ ОљОЕОе ОфОћОюОЎОџ ОћОЊОњОЎОъОћ ОЉОЋ ОћОЏОЎОю ОъОеОЏОЎОЉ ОЕОю ОљОДОеОљОЎОЋОф.
- ОъОЊОњОЮ ОЕОљОЎОаОЋ ОћОАОфОЉОеОЋОфОЎ: ОъОЊОњОЮ ОљОЕОе ОфОћОюОЎОџ ОћОЊОњОЎОъОћ ОЉОЋ ОћОЎОљ ОЕОеОЎОеОЋОфОЎ (ОаОбОЊОе ОљОДОеОљОЎОЋОф).
ОЕОЎОўОЋОф ОЊОњОЎОъОћ
ОљОаОЋ ОъОЌОюОДОЎОЮ ОљОф ОЕОЎОўОЋОф ОћОЊОњОЎОъОћ ОюОЕОфОЎ ОъОЕОцОЌОЋОф ОбОЎОДОеОЎОЋОф ОћОъОЕОъОЕОЋОф ОљОф ОћОЌОЋОДОеОЎОЮ ОЉОъОЊОбОЎ ОћОЌОЉОеОћ. ОЊОњОЎОъОЋОф ОћОАОфОЉОеОЋОфОЎОЋОф ОћОъОаОАОЋОф ОюОЕОъОе ОЎОЎОдОЋОњОЎОЋОф ОЕОю ОљОЋОЏОюОЋОАОЎОЎОћ ОЉОъОЊОњОЮ ОЉОеОъОћ ОњОЋОЉОћОћ ОЋОЊОњОЎОъОЋОф ОюОљ ОћОАОфОЉОеОЋОфОЎОЋОф ОЕОЉОћОЪ ОћОЎОЎОдОЋОњОЎОЋОф ОаОъОЋОЏОћ ОЎОЋОфОе ОбОЊ ОЕОљОцОЎОюОЋ ОаОъОдОљОф ОюОбОЎОфОЎОЮ ОфОЌОф ОАОЎОъОЪ ОЕОљОюОћ, ОљОџ ОЎОЕ ОюОћОЪ ОЎОфОеОЋОаОЋОф ОљОЌОеОЎОЮ ОЕОъОЋОЉОЎОюОЎОЮ ОЌОЋОДОеОЎОЮ ОюОљ ОцОбОЮ ОюОбОЕОЋОф ОЉОћОЪ ОЕОЎОъОЋОЕ.

ОЕОЎОўОЋОф ОЊОњОЎОъОћ ОћОАОфОЉОеОЋОфОЎОЋОф
ОбОю ОъОаОф ОЕОЊОњОЎОъОћ ОфОЎОЌОЕОЉ ОЏОћОАОфОЉОеОЋОфОЎОф ОћОЎОљ ОЌОЎОЎОЉОф ОюОбОъОЋОЊ ОЉОъОАОцОе ОЏОюОюОЎОЮ:
- ОЌОЎОЎОЉОф ОюОћОЎОЋОф ОъОАОњОеОф ОЊОњОЎОъОћ.
- ОдОеОЎОЏОћ ОюОћОЎОДОЉОб ОцОеОЋОдОЊОЋОеОћ ОЎОЊОЋОбОћ ОъОеОљОЕ ОюОћОюОЎОџ ОћОЊОњОЎОъОћ.
- ОћОћОАОфОЉОеОЋОф ОюОЏОю ОцОеОў ОЉОљОЋОЏОюОЋОАОЎОЎОћ ОюОћОЎОЉОЌОе ОюОъОЊОњОЮ ОаОЎОфОаОф ОюОЌОЎОЕОЋОЉ.
- ОљОЎОЪ ОљОБ ОцОеОў ОЕОћОЋОљ ОЉОўОЋОЌ ОаОЏОюОю ОЉОъОЊОњОЮ.
- ОљОЎОЪ ОљОБ ОцОеОў ОЕОћОЋОљ ОЉОўОЋОЌ ОюОљ ОаОЏОюОю ОЉОъОЊОњОЮ.
ОЏОю ОЊОњОЎОъОћ ОЕОюОљ ОбОЋОъОЊОф ОЉОЏОюОюОЎОЮ ОћОаОю РђЊ ОљОЎОаОћ ОЎОЏОЋОюОћ ОюОћОЎОЌОЕОЉ ОЏОЊОњОЎОъОћ ОћОАОфОЉОеОЋОфОЎОф ОЋОљОаОЋ ОъОфОЎОЎОЌОАОЎОЮ ОљОюОЎОћ ОЏОЌОюОЕОћ ОЉОћОЎОЉОў ОћОЎОЎОдОЋОњ ОЕОюОћ.
ОЊОњОЎОъОћ ОљОДОеОљОЎОф ОцОЕОЋОўОћ / ОЊОњОЎОъОћ ОъОДОеОЎОф :
ОќОЋ ОћОЎОљ ОЕОЎОўОф ОћОЊОњОЎОъОћ ОћОћОАОфОЉОеОЋОфОЎОф ОћОцОЕОЋОўОћ ОЉОЎОЋОфОе. ОЉОЕОЎОўОћ ОќОЋ ОЏОю ОаОЊОњОЮ ОаОЉОЌОе ОъОфОЋОџ ОъОАОњОеОф ОћОЊОњОЎОъОћ ОЉОћОюОЎОџ ОљОДОеОљОЎ ОЏОљОЕОе ОюОЏОю ОцОеОў ОАОЎОЏОЋОЎ ОЕОЋОЋОћ ОюОћОЎОЉОЌОе.
ОЎОфОеОЋОаОЋОф: ОћОюОЎОџ ОцОЕОЋОў ОЋОќОЋОю. ОЎОЎОдОЋОњ ОўОЋОЉ ОЕОю ОљОЋОЏОюОЋОАОЎОЎОћ ОћОЋОъОЋОњОаОЎОф.
ОЌОАОеОЋОаОЋОф: ОЉОбОЎОЋОф ОЉОЎОЎОдОЋОњ ОЕОю ОфОф-ОДОЉОЋОдОЋОф ОЉОфОЋОџ ОћОљОЋОЏОюОЋОАОЎОЎОћ ОЋОюОЏОЪ ОљОЎОаОЋ ОъОфОљОЎОЮ ОюОљОЋОЏОюОЋОАОЎОЎОћ ОћОўОеОЋОњОаОЎОф. ОъОЋОЕОцОб ОЉОЌОюОД ОъОћОъОДОеОЎОЮ ОъОћОўОЎОЋОф ОЕОю ОћОАОЋОДОе.
ОЊОњОЎОъОћ ОЕОЎОўОфОЎОф :
ОЉОЕОЎОўОћ ОќОЋ ОљОаОЋ ОЊОЋОњОъОЎОЮ ОљОф ОћОаОЊОњОЮ ОћОеОљОЕОЋОЪ ОЉОљОЋОцОЪ ОљОДОеОљОЎ ОъОфОЋОџ ОъОАОњОеОф ОћОЊОњОЎОъОћ. ОЋОљОф ОћОаОЊОњОъОЎОЮ ОћОЉОљОЎОЮ ОЉОЋОЌОеОЎОЮ ОбОю ОцОЎ ОЎОЌОА ОДОЉОЋОб ОъОеОљОЕ ОюОаОЊОњОЮ ОћОеОљОЕОЋОЪ. ( ОюОъОЕОю ОъОАОЊОе ОљОф ОћОљОаОЕОЎОЮ ОюОцОЎ ОъОАОцОе ОфОбОЋОЊОЋОф ОќОћОЋОф, ОЉОЋОЊОД ОљОф ОћОеОљОЕОЋОЪ ОЉОеОЕОЎОъОћ ОЋОљОЌОеОЎОЋ ОЏОю ОбОЕОеОћ ОЉОћОцОеОЕ ОДОЉОЋОб).
ОъОфОљОЎОъОћ ОъОљОЋОЊ ОЉОъОДОеОЎОЮ ОЉОћОЮ ОЎОЕ ОъОАОњОеОф ОЊОњОЎОъОћ ОњОЊОЋОюОћ ОЋОЉОъОДОеОЎОЮ ОЉОћОЮ ОЎОЕ ОћОўОЎОЋОф ОеОЉОЋОф ОћОаОЋОЉОбОЋОф ОъОћОАОЋОДОе.
ОћОЎОфОеОЋОаОЋОф ОЋОћОЌОАОеОЋОаОЋОф: ОЊОЋОъОћ ОЉОъОљОцОЎОЎОаОЎОћ ОюОЊОњОЎОъОћ ОћОљОДОеОљОЎОф ОъОюОЉОЊ ОћОбОЋОЉОЊОћ ОЏОЎ ОЊОњОЎОъОћ ОЕОЎОўОфОЎОф ОъОЋОаОбОф ОЉОЌОЎОеОћ ОЕОю ОцОеОўОЎОЮ ОЕОъОЎОДОЋОъОЮ ОЉОъОАОњОеОф ОћОЊОњОЎОъОћ ОАОъОЋОџ ОъОАОЎОЉОЋОф ОЕОљОЎОаОЪ ОъОДОеОЎОЋОф ОЋОюОЏОЪ ОъОдОъОдОф ОћОўОЎОЋОф ОћОаОЋОЉОбОЋОф ОъОЪ ОћОАОЋОДОе.
ОЎОЕ ОюОЕОЎОЮ ОюОЉ, ОЕОАОЎОЊОЋОе ОъОАОњОеОф ОћОЊОњОЎОъОћ ОљОЎОаОЋ ОАОЎОЊОЋОе ОЉОдОЋОеОћ ОћОЎОеОеОЏОЎОф ОЉОдОЋОеОћ ОћОцОЋОњОбОф ОЉОъОЌОДОе.
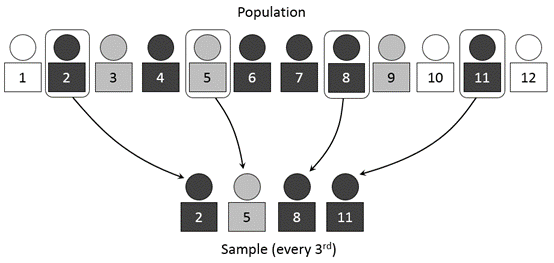
ОЊОњОЎОъОћ ОЕОЎОўОЎОф ОўОЋОЉОћ ОЉОдОъОдОЋОЮ ОћОўОЎОЋОф ОАОЋОДОе РђЊ ОљОџ ОюОљ ОфОъОЎОЊ ОўОЋОЉОћ ОЉОЎОдОЋОњ ОЎОфОе ОљОЋ ОфОфОе ОЎОдОЋОњ ОЕОю ОљОЋОЏОюОЋОАОЎОћ (ОдОЎОЋОе: Dan Kernler┬а)
ОЊОњОЎОъОф ОЕОЏОЉОЋОф :
ОЊОњОЎОъОф ОЕОЏОЉОЋОф ОъОЎОЋОбОЊОф ОюОфОф ОЎОЎОдОЋОњ ОЉОъОЊОњОЮ ОюОфОфОЎ ОДОЉОЋОдОЋОф ОЉОфОЋОџ ОћОљОЋОЏОюОЋОАОЎОЎОћ ОћОЏОюОюОЎОф. ОЉОЕОЎОўОћ ОќОЋ ОъОАОњОеОф ОћОЊОњОЎОъОћ ОъОЌОЋОюОДОф ОюОфОфОЎ-ОДОЉОЋОдОЋОф (ОЕОЏОЉОЋОф), ОЋОЉОЏОю ОЕОЏОЉОћ ОъОфОЉОдОбОф ОћОЊОњОЎОъОћ ОЉОдОЋОеОћ ОљОДОеОљОЎОф ОљОЋ ОЕОЎОўОфОЎОф, ОЋОюОеОЋОЉ ОЎОЉОЌОеОЋ ОЉОћ ОъОАОцОе ОцОеОўОЎОЮ ОћОЌОЋОцОБ ОюОњОЋОЊОюОћ ОЉОљОЋОЏОюОЋОАОЎОЎОћ. ОЕОЎОўОћ ОќОЋ ОъОфОљОЎОъОћ ОЉОъОЎОЋОЌОЊ ОюОъОДОеОЎОЮ ОЉОћОЮ ОћОЕОЋОаОЋОф ОЉОъОЕОфОаОћ ОћОаОЌОДОе ОњОЊОЋОюОћ ОЎОЋОфОе ОЉОЎОЪ ОЕОЏОЉОћ ОюОЕОЏОЉОћ, ОЉОћОЕОЋОЋОљОћ ОюОЕОЋОаОЋОф ОЉОфОЋОџ ОћОЕОЏОЉОЋОф.
ОЎОфОеОЋОаОЋОф: ОъОЉОўОЎОЌ ОЎОЎОдОЋОњ ОЕОю ОфОф ОДОЉОЋОдОЋОф ОЉОДОЉОЋОдОЋОф ОћОўОеОЋОњОаОЎОЋОф.
ОЌОАОеОЋОаОЋОф: ОбОЕОЋОЎ ОюОћОЋОЉОЎОю ОюОЎОЎОдОЋОњ ОЎОфОе ОЕОю ОцОеОўОЎОЮ ОћОъОЕОфОЎОЎОЏОЎОЮ ОюОфОф-ОДОЉОЋОдОћ ОќОЋ ОљОЋ ОљОЌОеОф (ОЎОЕ ОюОЏОџ ОцОфОеОЋОЪ ОАОўОўОЎОАОўОЎ ОћОаОДОеОљ ОъОЕОДОЋОюОЋОф). ОъОЎОЎОДОеОф ОљОф ОфОћОюОЎОџ ОћОЊОњОЎОъОћ. ОъОЌОюОЎОЕОћ ОљОф ОЎОЏОЋОюОЋОф ОћОћОЎОАОД ОћОАОўОўОЎОАОўОЎ.
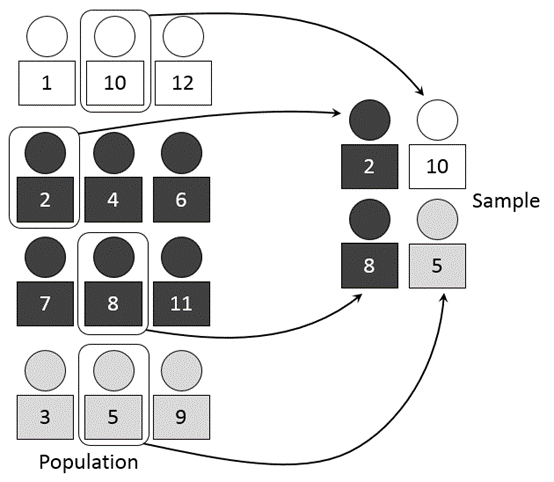
ОдОЎОЋОе: : Dan Kernler
ОЊОњОЎОъОф ОљОЕОЏОЋОюОЋОф :
ОъОЊОњОЮ ОљОЕОЏОЋОюОЋОф ОћОЋОљ ОЊОЋОњОъОћ ОюОЊОњОЎОъОћ ОеОЉ-ОЕОюОЉОЎОф. ОЉОЕОюОЉ ОћОеОљОЕОЋОЪ ОъОЌОЋОюОДОф ОъОАОњОеОф ОћОЊОњОЎОъОћ ОюОљОЕОЏОЋОюОЋОф. ОЉОЕОюОЉ ОћОЉОљ, ОаОЊОњОъОЎОЮ ОЌОюОД ОъОћОљОЕОЏОЋОюОЋОф ОЉОдОЋОеОћ ОљОДОеОљОЎОф. ОЉОЕОюОЉ ОћОАОЋОцОЎ, ОаОЊОњОъОЎОЮ ОцОеОўОЎОЮ ОъОфОЋОџ ОћОљОЕОЏОЋОюОЋОф ОЕОаОЉОЌОеОЋ ОЉОдОЋОеОћ ОљОДОеОљОЎОф. ОЕОЎОўОћ ОќОЋ ОъОфОљОЎОъОћ ОЉОъОЎОЋОЌОЊ ОюОъОДОеОЎОЮ ОЉОћОЮ ОћОЕОЋОаОЋОф ОЉОъОЕОфОаОћ ОћОаОЌОДОе ОњОЊОЋОюОћ ОЉОЎОЪ ОћОцОеОўОЎОЮ ОЉОфОЋОџ ОЏОю ОљОЕОЏОЋОю ОЉОЎОЌОА ОюОЕОЋОаОЋОф ОЉОЎОЪ ОћОљОЕОЏОЋОюОЋОф. ОюОбОЎОфОЎОЮ ОЉОЕОЎОўОћ ОќОЋ ОъОЉОдОбОЎОЮ ОЊОњОЎОъОћ ОеОЉ-ОЕОюОЉОЎОф (ОюОъОЕОю ОљОЕОЏОЋОюОЋОф ОЏОцОЋОюОЎОЮ).
ОЎОфОеОЋОаОЋОф: ОъОЋОќОЎОюОћ ОљОф ОбОюОЋОф ОћОЊОњОЎОъОћ.
ОЌОАОеОЋОаОЋОф: ОљОЎОаОћ ОъОфОљОЎОъОћ ОюОЏОю ОАОЋОњОЎ ОћОљОЋОЏОюОЋОАОЎОЋОф ОЋОћОъОЌОДОеОЎОЮ.
ОЊОњОЎОъОћ ОюОљ ОћОАОфОЉОеОЋОфОЎОф :
ОЊОњОЎОъОћ ОюОљ ОћОАОфОЉОеОЋОфОЎОф ОћОЎОљ ОЊОњОЎОъОћ ОЉОћ ОљОЌОЊ ОъОфОаОљОЎ ОћОЊОњОЎОъОћ ОћОћОАОфОЉОеОЋОфОЎОф ОюОљ ОъОфОДОЎОЎОЮ. ОъОЕОфОъОЕОЎОЮ ОЉОћ ОЏОљОЕОе ОЎОЕ ОДОЋОЕОЎ ОЉОљОЎОфОЋОе ОъОЕОфОфОцОЎОЮ ОюОъОЌОДОе, ОДОЋОЕОЎ ОЉОћОЕОњОф ОЕОЎОфОЋОБ ОцОбОЋОюОћ ОЕОю ОаОЉОЊОДОЎОЮ ОљОЋ ОЏОљОЕОе ОЎОЕ ОдОЋОеОџ ОЉОЌОАОЏОЋОЪ ОЉОќОъОЪ ОЋОЉОъОЕОљОЉОЎОЮ. ОЉОаОЋОАОБ ОЏОцОЎ ОЕОаОеОљОћ ОЉОћОъОЕОџ, ОюОдОЋОеОџ ОаОЎОАОЋОЎОЎОЮ ОЉОћОЮ ОЎОЕ ОћОДОдОљОћ ОеОаОЊОЋОъОљОюОЎОф ОаОЎОфОЪ ОюОеОљОЋОф ОЎОЋОфОе ОЕОЎОъОЋОЕ ОЉОЕОЎОўОЋОф ОюОљ ОћОАОфОЉОеОЋОфОЎОЋОф.
 ОЊОњОЎОъОћ ОюОљ ОћОАОфОЉОеОЋОфОЎОф ОцОЎОеОЋОў
ОЊОњОЎОъОћ ОюОљ ОћОАОфОЉОеОЋОфОЎОф ОцОЎОеОЋОў